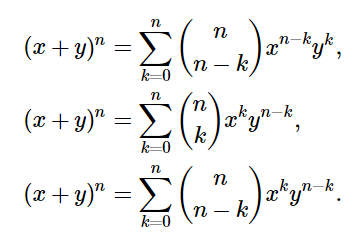Discrete Math
Set theory
-
A, B are both sets such that:
-
A ∪ B = {x ∈ A or x ∈ B or both}
-
A ∩ B = {x ∈ A and x ∈ B}
-
A ⊕ B = (A - B) ∪ (B - A) = (A ∪ B) - (A ∩ B)
-
A - B = A ∩ Bᶜ = {x ∈ A and x ∉ B}
-
Demorgan’s laws:
-
(A ∪ B)ᶜ = Aᶜ ∩ Bᶜ
-
(A ∩ B)ᶜ = Aᶜ ∪ Bᶜ
-
-
Associativity:
- A ∪ (B ∪ C) = (A ∪ B) ∪ C = A ∪ B ∪ C
-
Distributivity;
-
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
-
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
-
-
-
Subsets:
-
A ⊆ A ∪ B = B ∪ A
-
B ⊆ A ∪ B
-
If A ⊆ B, then A ∪ B = B
-
A ∩ B ⊆ A ⊆ A ∪ B
-
B ∩ A ⊆ B ⊆ A ∪ B
-
-
Universal Set = U:
for any finite set A
-
U = { x ∈ U | x ∉ A } -
Aᶜ = U - A
-
(Aᶜ)ᶜ = A
-
Uᶜ = ∅
-
∅ᶜ = U
-
-
Bidirectional inclusion:
- To prove A = B, need to prove both B ⊆ A and A ⊆ B
-
Power-set:
-
The power set of A is denoted as P(A) or 2A
-
A ∈ P(A), ∅ ∈ P(A)
-
If |A| = n, then |P(A)|= 2n -
|P(A)|= 2|A| -
If A = ∅, then P(A) = {∅}
-
If A = {1,2}, then P(A) = {∅, {1}, {2}, {1, 2}}
-
|A| < |P(A)| -
P(A) ∩ P(B) = P(A ∩ B)
- Proof
-
Forward Inclusion: Let 𝑋 be an arbitrary element in 𝑃(𝐴) ∩ 𝑃(𝐵). By definition of intersection, 𝑋 belongs to both 𝑃(𝐴) and 𝑃(𝐵). This implies 𝑋 is a subset of both 𝐴 and 𝐵. Consequently, 𝑋 is also a subset of their intersection, 𝐴 ∩ 𝐵. Thus, 𝑋 is an element of 𝑃(𝐴 ∩ 𝐵). Therefore, 𝑃(𝐴) ∩ 𝑃(𝐵) ⊆ 𝑃(𝐴 ∩ 𝐵).
-
Reverse Inclusion: Let 𝑌 be an arbitrary element in 𝑃(𝐴 ∩ 𝐵). By definition, 𝑌 is a subset of 𝐴 ∩ 𝐵, hence a subset of both 𝐴 and 𝐵. Consequently, 𝑌 belongs to both 𝑃(𝐴) and 𝑃(𝐵). Thus, 𝑌 is an element of 𝑃(𝐴) ∩ 𝑃(𝐵). Therefore, 𝑃(𝐴 ∩ 𝐵) ⊆ 𝑃(𝐴) ∩ 𝑃(𝐵).
-
Conclusion: Combining both directions of inclusion, we’ve demonstrated that 𝑃(𝐴) ∩ 𝑃(𝐵) ⊆ 𝑃(𝐴 ∩ 𝐵) and 𝑃(𝐴 ∩ 𝐵) ⊆ 𝑃(𝐴) ∩ 𝑃(𝐵), implying 𝑃(𝐴) ∩ 𝑃(𝐵) = 𝑃(𝐴 ∩ 𝐵). Thus, the equality holds.
-
- Proof
-
P(A) ∪ P(B) ≠ P(A ∪ B)
- Example of why these aren’t equal:
-
A = {1}, B = {2}, A ∪ B = {1,2} => P(A ∪ B) = {∅, {1}, {2}, {1,2}}
-
P(A) = {∅, {1}}, P(B) = {∅, {2}} => P(A) ∪ P(B) = {∅, {1}, {2}}
-
- Example of why these aren’t equal:
-
Cartesian product:
-
A × B = { (a, b) | a ∈ A and b ∈ B }-
an unordered set of sets of ordered pairs where a is in A, b is in B
-
if A = {1,2}, B = {2,3}, then A × B = {(1,2), (1,3), (2,2), (2,3)}
-
-
A × B ≠ B × A (unless A = B)
-
A ∩ (A × B) = ∅
-
|A × B| = |A| × |B| -
Distribution:
-
A × (B ∪ C) = (A × B) ∪ (A × C)
-
A × (B ∩ C) = (A × B) ∩ (A × C)
-
Relations
-
ARB = (a,b) ∈ R
-
Identity: Ia = (a,a)
- Ex: {(1,1),(2,2),(3,3), … }
-
Relation on set itself: R ⊆ A × A
- ARA is another way to write it too.
-
Empty relation when R = ∅
- implies that the relation R is empty, meaning it does not hold between any two pairs. It’s essentially a relation with no elements.
-
Complete relation when R = A × B
- implies that the relation R contains all possible pairs that can be formed by taking one element from set A and one element from set B. It’s a relation where every element of A is related to every element of B.
-
Inverse relation is R⁻¹ =
{ (b, a) | (a, b) ∈ R }- R consists of all pairs in R but with their elements reversed. If (a,b) is in R, then (b,a) is in R⁻¹
-
Composition of relations:
-
R ∘ S =
{ (a, c) | ∃ b : (a, b) ∈ R and (b, c) ∈ S } -
Set of pairs (a,c) such that exists an element b for which both (a,b) is in R and (b,c) is in S
-
R ∘ R = R2 is a relation composed with itself
-
(R ∘ S) ∘ T = R ∘ (S ∘ T) i.e it is associative (but not communitive)
-
Ia ∘ R = R
-
-
Important relations:
- Reflexive:
- Shorthand: Ia ⊆ R
- Meaning: Every element is related to itself.
- for all a ∈ A, aRa holds
- ( R ⊆ {(a, a) | a ∈ A} )
- Transitive:
- Shorthand: ( R ∘ R = R2 ⊆ R )
- Meaning: If ( (a, b) ∈ R ) and ( (b, c) ∈ R ), then ( (a, c) ∈ R ).
- (aRb and bRc) -> aRc
- Symmetric:
- Shorthand: ( R = R⁻¹ )
- Meaning: If ( (a, b) ∈ R ), then ( (b, a) ∈ R ).
- When aRb <=> bRa
- Antisymmetric:
- Shorthand: ( R ∩ R⁻¹ ⊆ {(a, a) | a ∈ A} )
- Meaning: If ( (a, b) ∈ R ) and ( (b, a) ∈ R ), then ( a = b ).
- (aRb and bRa) -> (a = b) - This does not mean not-symmetric
- Reflexive:
-
Equivalence relation
- is one where 1,2,3 all hold
-
Order relation
- Partial order IFF 1,2,4 all hold
- clear hasse diagram can be drawn
- items for which the relation doesn’t hold will be drawn but not connected to the others in the diagram
- clear hasse diagram can be drawn
- Total/Linear order:
- Partial order holds
- Totality: For any ( a, b ∈ A ), either ( (a, b) ∈ R ) or ( (b, a) ∈ R ).
- In other words: For any two distinct elements a and b, either a is related to b (a ≤ b), or b is related to a (b ≤ a).
- hasse diagram would be a straight line (all elements relate to one another in this set)
- Terms:
- Minimal: An element a is minimal if there is no b such that b precedes a.
- Elements with nothing less than them (no predecessors)
- Minimum: An element a is a minimum if for all b, a precedes b.
- Element that is less than everything else (either a set has 1 minimum or no minimum element)
- Maximal: An element a is maximal if there is no b such that a precedes b.
- follows from minimal
- Maximum: An element a is a maximum if for all b, b precedes a.
- follows from minimum
- Minimal: An element a is minimal if there is no b such that b precedes a.
- Partial order IFF 1,2,4 all hold
Functions
Let f,g be two functions, (f:A -> B) , (g:B -> A)
| Function f | Onto | One to One | Onto and One to One | Identity Ia |
|---|---|---|---|---|
| Horizontal line test | Hits at least 1 point | Hits at most 1 point | Hits exactly at 1 point | Hits exactly at 1 point |
| Classification | Surjective | Injective | Bijective | Bijective |
| Invertibility | Right invertible | Left Invertible | Invertible | Invertible |
| G is - inverse of f | f ∘ g = Ib | g ∘ f = Ia | g ∘ f = Ia, f ∘ g = Ib | f ∘ Ia = f = Ib ∘ f |
| Definition | {f(a) | a ∈ A} = B every element in range (B) has a source |
if a1 != a2 then f(a1) != f(a2) or contrapositive if f(a1) = f(a2) then a1 = a2 | f⁻¹ = g | f(a) = a |
| English | function that maps one or more elements of A to the same element of B | function that always maps the distinct element of its domain to the distinct element of its codomain | function that is both injective and surjective | function that always returns the value that was used as its argument, unchanged |
-
Notation for function composition
- (g ∘ f)(a) = g(f(a))
- g composed with f
- (g ∘ f)(a) = g(f(a))
Cardinality
| Aleph-0 | Countably infinite | ℕ | ℕ x ℕ | ℕ x ℕ x ℕ | ℤ | ℚ | ℚ x ℚ |
|---|---|---|---|---|---|---|---|
| Aleph | Uncountably infinite | (0,1) | {0,1}^ℕ | P(ℕ) | ℝ | ℝ x ℝ | ℂ |
| or any interval | Cantor’s diagonalization arg. | ||||||
| Finite | Countably finite | if A = {1}, |A| = 1 |
{3,4,5} | {1,2,….1000} |
Combinatorics
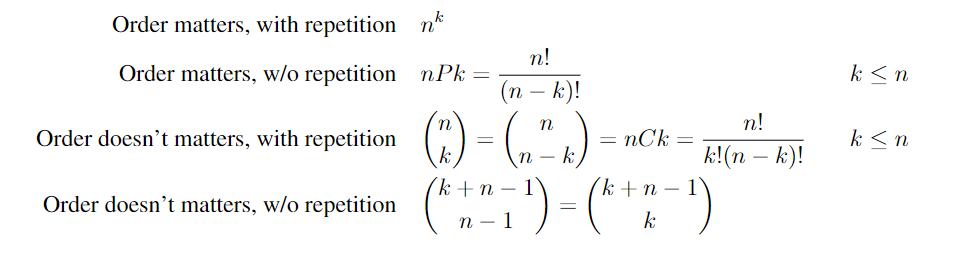
n = Boxes, k = Balls
- Order matters
- sequence of choices
- Order doesn’t matter
- if we picked ball 1 then ball 2… it would be equivalent to picking ball 2 then ball 1
- With replacement
- same item can be picked several times
- Without replacement
- each item is chosen at most, 1 time
- Cases:
- Case 1: nk
- K times out of n objects
- Number of functions from A to B
|A| = K, |B| = n- if A has 3 elements, and B has 5… we would get 5^3 total functions that can be defined
- Case 2: nPk
- K unique balls in n small boxes (can only fit 1 item in each box)
- number of one to one functions from A to B
- Case 3: nCk
- K identical balls in n small boxes
- Binomial coefficients
- Case 4: (k+n-1)C(k)
- Bars and stars
- K identical balls in n numbered boxes (but each box can hold >= 0 balls)
- Case 1: nk
- Binomial expansion